Куцик П.О., Миронов Ю.Б., Башнянин Г.І. Рейтингування діяльності банківських установ як інструмент стабілізації національної економіки
Розділ 2. Вплив надійності банківського рейтингування на стабілізацію національної економіки
2.1. Показники оцінювання точності банківських рейтингів
Для перевірки правильності розроблених методик рейтингування банків необхідно періодично здійснювати оцінювання їх ефективності, що вимагає формування статистичної бази даних щодо присвоєних рейтингів і фактичних дефолтів. У закордонній практиці для цього використовуються такі показники, як профіль акумульованої точності (ПАТ) і коефіцієнт передбачуваної здатності (КПЗ) [28, c.72].
Сутність КПЗ полягає в розрахунку інтегрального коефіцієнта на основі порівняння присвоєних рейтингів з кількістю фактичних дефолтів. Із цією метою всіх позичальників поділяють на дві групи: ті, які виконали свої зобов’язання, і ті, які їх не виконали. Як правило, зобов’язання вважаються невиконаними, якщо платіж не здійснено протягом 30 днів після встановленого в договорі терміну сплати зобов’язань. Рейтинги суб’єктів господарювання з цих груп порівнюються попарно.
У результаті порівняння кожної пари їй присвоюється числове значення R(ij) за таким алгоритмом:
- R(ij) = 1, якщо початковий рейтинг позичальника (і), який не виконав своїх зобов’язань, був гіршим за рейтинг позичальника (j), який свої зобов’язання виконав;
- R(ij) = 0,5, якщо рейтинги збігаються;
- R(ij) = 0, якщо початковий рейтинг позичальника (і), який не виконав своїх зобов’язань, був кращим за рейтинг позичальника (j), який свої зобов’язання виконав.
Кількість пар, що порівнюються, визначається добутком кількостей позичальників, які не виконали своїх зобов’язань, та тих, які виконали свої зобов’язання.
Показник КПЗ розраховується за формулою
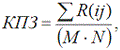 (2.1)
(2.1)
де М – кількість позичальників, які не виконали своїх зобов’язань; N – кількість позичальників, які свої зобов’язання виконали [112].
Рейтингові системи, для яких значення КПЗ перевищує 0,5, можна вважати ефективними, тобто такими, що дають адекватну, достовірну, точну оцінку кредитного рейтингу [28, c.73].
Крива ПАТ (cumulative accuracy profile – CAP) – це візуальний інструмент, який використовує РА «Moody’s» для оцінювання ефективності рейтингових систем. Алгоритм побудови кривої ПАТ подібний до алгоритмів побудови відомих в економічній науці кривої Джині та кривої Лоренца. Крива ПАТ також зустрічається в літературі під назвою силової кривої («power curve») [185]. На першому етапі побудови кривої ПАТ усі спостереження рейтингових оцінок упорядковуються від найгіршого рейтингового класу до найкращого. У випадку бальної (скорингової) рейтингової моделі, коли найкращий рейтинговий клас присвоюється банкам з найбільшою кількістю балів, а найгірший – банкам з найменшою кількістю балів, усі спостереження банківських рейтингів упорядковуються за зростанням бальної оцінки (S). Для кожного бального класу оцінюються такі ймовірності:
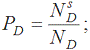 (2.2)
(2.2)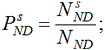 (2.3)
(2.3)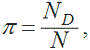 (2.5)
(2.5)
де PDs – ймовірність того, що збанкрутілий банк має S балів; PNDs – ймовірність того, що незбанкрутілий банк має S балів; PTs – ймовірність того, що банк має S балів; π – ймовірність банкрутства у загальній сукупності банків; ND – кількість збанкрутілих банків у загальній сукупності; NND – кількість незбанкрутілих банків у загальній сукупності; N – загальна кількість банків; NDs – кількість збанкрутілих банків, які мають S балів; NNDs – кількість незбанкрутілих банків, які мають S балів.
Для кожної бальної оцінки (рейтингового класу) оцінюються кумулятивні ймовірності:
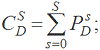 (2.6)
(2.6)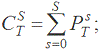 (2.7)
(2.7)
де CDS – ймовірність того, що збанкрутілий банк має менше S балів; CTS – ймовірність того, що банк має менше S балів.
Після розрахунку цих ймовірностей за формулами (2.2-2.7) будується крива ПАТ, яка є графіком усіх точок CDS та CTS для кожної бальної оцінки (рейтингового класу). Уздовж осі x відкладається CTS, а уздовж осі y – CDS. Випадкова рейтингова модель, яка не матиме здатності розрізняти різні рівні ймовірностей банкрутства між рейтинговими класами, буде представлена на графіку діагональною прямою: y = x. Ідеальна рейтингова модель надаватиме збанкрутілим банкам найнижчі рейтингові класи. Крива ПАТ для ідеальної рейтингової моделі матиме вигляд кривої, яка буде максимально наближатися до ламаної лінії: (0.0)-(0.1)-(1.1). Крива ПАТ для реальної рейтингової моделі лежатиме між діагоналлю та кривою ПАТ для ідеальної моделі. На рис. 2.1 наведено приклад графіка кривої ПАТ.
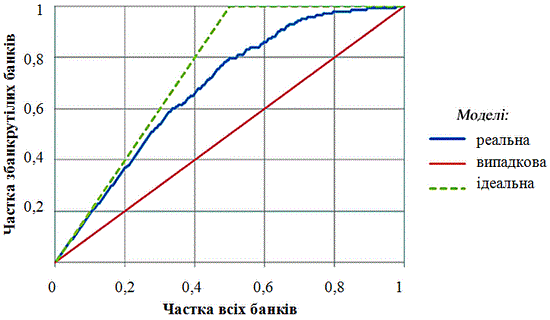
З рис. 2.1 видно, що криві ПАТ можуть бути використані як візуальний інструмент для порівняння точностей різних систем банківських рейтингів. Проте основною перевагою кривих ПАТ є можливість розрахунку на їх основі рівнів точностей (РТ) банківських рейтингів. Рівні точностей різних банківських рейтингів дають однозначну числову характеристику надійності того чи іншого банківського рейтингу.
Порівнюючи ступені точностей, можна однозначно оцінити, яка рейтин-гова система присвоює надійні рейтинги. Рейтингова система може включати помилки двох типів:
- помилка першого типу полягає у тому, що банку не присвоюється дефолтна рейтингова категорія при тому, що банк банкрутує;
- помилка другого типу полягає в тому, що банку присвоюється дефолтна рейтингова категорія при тому, що банк не банкрутує. Оцінити відносний обсяг таких помилок дає змогу показник AR (accuracy ratio), який розраховується за формулою
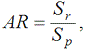 (2.8)
(2.8)
де Sr – площа між кривою ПАТ реальної моделі присвоєння банківських рейтингів і кривою ПАТ випадкової моделі (діагональ); Sp – площа між кривою ПАТ ідеальної моделі присвоєння банківських рейтингів і кривою ПАТ випадкової моделі.
Рівень точності (AR) набуває значень між 0 та 1: що вище значення AR, то надійнішим є банківський рейтинг. Рівень точності (AR) можна розрахувати за формулою
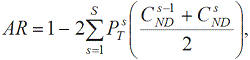 (2.9)
(2.9)де CNDS – ймовірність того, що незбанкрутілий банк має менше S балів.
Ще одним візуальним інструментом оцінювання надійності банківських рейтингів є крива робочих характеристик отримувача або ROC крива (ROC – receiver operating characteristic). У контексті теми дослідження під отримувачем розуміється система присвоєння банківських рейтингів, яка отримує інформацію від банків, наприклад, у формі фінансових показників цих банків. Залежно від внутрішніх параметрів системи присвоєння банківських рейтингів на виході цієї системи будуть різні результати у формі присвоєних рейтингів. Залежність якості отриманих результатів від внутрішніх параметрів системи і є кривою робочих характеристик отримувача, яка дає змогу встановити оптимальні внутрішні параметри системи (отримувача). Щоб зрозуміти суть цього інструмента, необхідно уявити особу, яка ухвалює рішення про присвоєння банкам певної рейтингової категорії, така особа намагається спрогнозувати стан кожного банку в майбутньому періоді. Для ухвалення рішення така особа має у своєму розпорядженні бальні оцінки фінансового стану кожного банку. Особі, яка ухвалює рішення, необхідно встановити граничне значення бальної оцінки таким чином, що банки з бальною оцінкою нижче цього граничного значення класифікуються як потенційні банкрути, а банки з бальною оцінкою вище граничного значення класифікуються як надійні фінансові установи. Порівнявши статистику банкрутств у майбутньому періоді із зробленим прогнозом, можна оцінити ефективність методики присвоєння бальної оцінки банкам і відповідного граничного значення. Позначимо через Score бальну оцінку, яку отримує кожний банк, а через x – граничне значення бальної оцінки для класифікації банків. Для кожного банку в прогнозному періоді можливі чотири сценарії (табл. 2.1).
Таблиця 2.1. Можливі сценарії для кожного банку в прогнозному періоді
| Фінансовий стан банку в прогнозному періоді | Score < x | Score > x |
| Дефолтний | Істинний прогноз (сценарій А) | Помилковий прогноз (сценарій Б) |
| Стабільний | Помилковий прогноз (сценарій В) | Істинний прогноз (сценарій Г) |
Сценарій А полягає в тому, що банк із балом нижче граничного значення дійсно збанкрутує в майбутньому (прогнозному) періоді. Сценарій Б полягає в тому, що банк із балом вище граничного значення збанкрутує в майбутньому періоді, хоча був класифікований як надійний банк. Сценарій Б є помилкою першого типу. Сценарій В полягає в тому, що банк із балом нижче граничного значення не збанкрутує в майбутньому, хоча був класифікований як ненадійний. Сценарій В є помилкою другого типу. Сценарій Г полягає в тому, що банк із балом вище граничного значення не збанкрутує в майбутньому періоді, відповідно зроблений прогноз справдиться.
Залежно від граничного значення x розраховується рівень правильно спрогнозованих дефолтів HR(x):
......................
* * * * * *
......................
Значення E[AT] знаходиться із системи рівнянь (2.27), при цьому значення обсягу власного капіталу банку (Е) та обсяг зобов’язань (Х) беруться з відкритої фінансової звітності банку, а показники динаміки ринкової вартості активів банку (µ, σ) розраховуються на основі даних фондових бірж про динаміку цін на акції банку.
На практиці найчастіше використовують саме другий метод. Використовує його і «Moody’s KMV» для розрахунку свого фірмового показника EDF. Як уже згадувалося, «Moody’s KMV» для розрахунку EDF використовує VK-модель, яка усуває деякі спрощення та обмеження класичної моделі Мертона. Детально VK-модель висвітлена в працях Кросбі та Бона [177], Васічека [209] та Кілгофера [184]. Особливістю VK-моделі є те, що вартість власного капіталу банку моделюється як безкінечний бар’єрний опціон (perpetual down-and-out option) на вартість активів цього банку. Також ця модель передбачає виокремлення п’яти різних типів зобов’язань: короткострокових, довгострокових, конвертованого боргу, привілейованих та звичайних акцій. Використовуючи розширений згідно з VK-моделлю варіант системи рівнянь (2.27), «Moody’s KMV» розраховує ринкову вартість активів банку та волатильність цієї ринкової вартості. VK-модель передбачає, що дефолтний поріг (ХT) змінюється в часі, тому його динаміка визначається емпірично. Відстань до дефолту (DDT) також змінюється з часом і розраховується за формулою
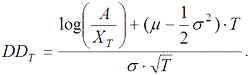 (2.30)
(2.30)Згідно з VK-моделлю, якщо ринкова вартість активів банку падає нижче дефолтного порога в будь-якій точці часу до моменту Т, то банк вважається збанкрутілим, у той час як за моделлю Мертона банк може збанкрутувати тільки в момент часу Т. Така особливість VK-моделі робить її більш наближеною до реальності порівняно з моделлю Мертона. Далі на основі статистичних відомостей про відстані до дефолтів та емпіричні рівні дефолтів будується кореляційна залежність очікуваної частоти дефолту (EDF) від відстані до дефолту, розрахованої за формулою (2.30). А вже на основі цієї кореляційної залежності, обчисливши для банку відстань до дефолту, визначаємо його показник EDF.
Отже, методика розрахунку показника EDF відрізняється від традиційної структурної моделі Мертона за такими напрямами:
- VK-модель розглядає банк як суб’єкт, який безперервно бере та повертає позики;
- розглядаються різні види зобов’язань банку, що дає змогу врахувати більше особливостей структури капіталу;
- розрахункова волатильність ринкової вартості активів банку виводиться з темпів приросту ринкової вартості активів, які, своєю чергою, розраховуються на основі темпів приросту балансової вартості власного капіталу. Це відрізняється від популярного підходу, який полягає в тому, що волатильність ринкової вартості активів розраховується шляхом мультиплікації волатильності балансової вартості власного капіталу;
- остаточна волатильність ринкової вартості активів визначається шляхом порівняння розрахункової волатильності ринкової вартості активів із модельною волатильністю, яка оцінена для інших подібних банків, тобто фільтрується шум у часовій серії вартості активів [164, с.7].
Концепція побудови показника порядкової помилки якості рейтингу ORQS спирається на припущення про те, що існує ідеальна, еталонна модель рейтингового оцінювання банків, а саме: модель розрахунку EDF, відносно якої і визначається надійність певної рейтингової системи. Проте, Д. Мунвес, Д. Гамільтон [199] та Р. Кантор, К. Ман [175] аргументовано критикують показник EDF, посилаючись на те, що абсолютні значення цього показника погано співвідносяться з фактичними дефолтними частотами, особливо в періоди фінансово-економічних криз. Відомі приклади, коли банки з EDF у 5% банкрутували, щоправда такі банки до банкрутства мали EDF на рівні до 0,1%, тобто для прогнозування банкрутства більше значення має відносна зміна показника EDF. Самі автори показника порядкової помилки якості рейтингу ORQS [181] визнають подібні недоліки такого «еталонного» показника надійності банку і наводять низку аргументів, які, на їх думку, нівелюють недоліки використання EDF як надійної оцінки кредитоспроможності банків.
Очевидно те, що модель рейтингового оцінювання банків, яка претендує на роль еталонної, повинна оцінювати (прогнозувати) емпіричну ймовірність дефолту у групі банків певної рейтингової категорії. Тоді для такої моделі можна розрахувати показник Бріера (формула (2.24)), який є найбільш об’єктивним критерієм надійності банківських рейтингів, тому що порівняння прогнозних (модельних) ймовірностей дефолтів із фактичними частотами дефолтів для різних рейтингових категорій є безпосереднім вимірником якості моделі прогнозування ймовірностей дефолтів. Проте дефолти банків є доволі рідкісним явищем, тому фактична частота дефолтів як випадкова величина матиме значну варіацію, що ускладнює побудову точних економіко-математичних моделей оцінювання ймовірностей дефолтів банків. Відповідно, на практиці часто доводиться приймати за еталонні моделі рейтингового оцінювання банків не дуже якісні моделі.
Для оцінювання впливу варіації частоти дефолтів у певній рейтинговій категорії на точність методики складання банківських рейтингів ми пропонуємо свій показник надійності банківських рейтингів – коефіцієнт детермінації для лінійної кореляційної залежності фактичної частоти дефолтів від середнього або медіанного значення бальної оцінки банків (KD). Для розрахунку KD припустімо, що існує сукупність із N банків, яким певна рейтингова система присвоює оцінки надійності S таким чином, що для найкращих банків значення S має бути мінімальним, а для найгірших – максимальним. Загальна кількість банків N ділиться випадковим чином на v рівних груп так, щоб до кожної групи потрапило не менше 30 банків, кількість банків у групі (k) становитиме k = N/v. Залежно від діапазону оцінок S банкам присвоюється n рейтингових класів, при цьому ai – мінімальне значення оцінки S для i-го рейтингового класу; bi – максимальне значення оцінки S для i-го рейтингового класу; i = 1...n. На кожному кроці j = 1...v кількість банків, що розглядається Qj = j·k, тобто з кожним кроком до розгляду кумулятивно залучається наступна група. Результати спостережень заносяться до табл. 2.2.
Таблиця 2.2. Зведення даних для розрахунку коефіцієнта детермінації для лінійної кореляційної залежності фактичної частоти дефолтів від середнього або медіанного значення бальної оцінки банків (KD)
| j | Qj | Рейтинговий клас, i | Діапазони оцінок, S | Кількість банків, qij | Кількість збанкрутілих банків, Dij | Медіана, або середнє значення, S, MSij | Фактична частота дефолтів, DFij |
| 1 | 1·k | 1 | (a1; b1) | q11 | D11 | MS11 | DF11=D11/q11 |
| 2 | (a2; b2) | q21 | D21 | MS21 | DF21=D21/q21 | ||
| i | (ai; bi) | qi1 | Di1 | MSi1 | DFi1=Di1/qi1 | ||
| n | (an; bn) | qn1 | Dn1 | MSn1 | DFn1=Dn1/qn1 | ||
| 2 | 2·k | 1 | (a1; b1) | q12 | D12 | MS12 | DF12=D12/q12 |
| 2 | (a2; b2) | q22 | D22 | MS22 | DF22=D22/q22 | ||
| i | (ai; bi) | qi2 | Di2 | MSi2 | DFi2=Di2/qi2 | ||
| n | (an; bn) | qn2 | Dn2 | MSn2 | DFn2=Dn2/qn2 | ||
| … | … | … | … | … | … | … | … |
| v | v·k | 1 | (a1; b1) | q1v | D1v | MS1v | DF1v=D1v/q1v |
| 2 | (a2; b2) | q2v | D2v | MS2v | DF2v=D2v/q2v | ||
| i | (ai; bi) | qiv | Div | MSiv | DFiv=Div/qiv | ||
| n | (an; bn) | qnv | Dnv | MSnv | DFnv=Dnv/qnv |
У табл. 2.2 qij – це кількість банків на j-му кроці, які потрапили до і-го рейтингового класу, оскільки їх оцінки S перебувають у межах від ai до bi; Dij – кількість фактично збанкрутілих банків серед банків і-го рейтингового класу на j-му кроці; MSij – медіанне, або середнє, значення оцінки S банків і-го рейтингового класу на j-му кроці; DFij – фактична частота дефолтів серед банків і-го рейтингового класу на j-му кроці, яка розраховується за формулою
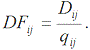 (2.31)
(2.31)Маючи значення MSij та DFij, ми методом найменших квадратів оцінюємо параметри h і h1 кореляційної залежності: DFt = h·MSt + h1, де t = 1...n·v, також перевіряємо значущість цих параметрів. На основі зазначеної кореляційної залежності знаходимо коефіцієнт детермінації (KD) за формулою
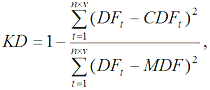 (2.32)
(2.32)де CDFt – відповідне розрахункове значення частоти дефолту, яке розраховується для MSt на основі розглянутої лінійної регресії 1-го порядку; MDF – середнє значення фактичної частоти дефолтів.
Показник KD перебуває в межах від 0 до 1: що більше його значення, то стійкішою є модель присвоєння банківських рейтингів до варіації фактичної частоти дефолтів. Низьке значення показника KD свідчить про необхідність перегляду калібровочних коефіцієнтів у моделі присвоєння банківських рейтингів. Отже, що більший показник KD, то краща відповідність абсолютних значень рейтингових оцінок фактичним частотам дефолтів, відповідно більш надійними є банківські рейтинги [94, с.29].
Основною проблемою при розробленні показників надійності банківських рейтингів є те, що в основу обчислення більшості з цих показників покладено розрахунок фактичних частот дефолтів. Оскільки відношення кількості дефолтів серед банків до їх загальної кількості є незначним, то фактичні частоти дефолтів будуть мати значну варіацію, що, своєю чергою, зменшує точність показників надійності банківських рейтингів. Для усунення цього недоліку ми пропонуємо будувати криву ПАТ (рис. 2.1) не за частками збанкрутілих банків, а за частками банків, рентабельність активів яких нижча від середньозваженої норми прибутку у банківському секторі даної країни. На основі такої модифікованої кривої ПАТ за формулами (2.8)-(2.9) можна визначити рівень точності, який ми пропонуємо називати ступенем точності за чистим прибутком (ARP), оскільки в основу розрахунку рентабельності активів банку покладено чистий прибуток. Отже, рівень точності банківських рейтингів за чистим прибутком розраховується за формулою
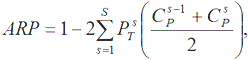 (2.33)
(2.33)
де CPS – ймовірність того, що банк, у якого рентабельність активів у прогнозному періоді вища за середньозважену за активами норму прибутку в банківському секторі, має менше S балів.
Що ближче значення ARP до 1, то точніші банківські рейтинги.
