Куцик П.О., Миронов Ю.Б., Башнянин Г.І. Рейтингування діяльності банківських установ як інструмент стабілізації національної економіки
Розділ 4. Формування та використання банківських рейтингів для стабілізації національної економіки
4.2. Методика розрахунку рейтингової оцінки банку
У попередньому підрозділі з великої кількості показників діяльності банків ми відібрали 132 найважливіших абсолютних і відносних показники, які можна розрахувати за відкритою фінансовою звітністю банків. Ці показники є незалежними факторними змінними в нашій загальній моделі перед фільтруванням, яку ми умовно позначаємо ЗМ-132. Залежно від вибору підсумкової залежної ознаки можна максимізувати той чи інший показник надійності банківських рейтингів. Для початку перевіряємо, чи можна спрогнозувати банкрутство банку в наступному кварталі за його фінансовими показниками в поточному кварталі. Для цього розглядаємо підсумкову змінну DF-1, яка набуває значення «0», якщо банк не банкрутує у наступному кварталі, і значення – «1», якщо банк банкрутує у наступному кварталі. Замість нуля та одиниці може бути певний рейтинговий клас або категорія, наприклад, «банкрутує» і «не банкрутує». Маючи квартальну відкриту фінансову звітність українських банків з 2009 р., ми отримуємо 3934 квартальних спостереження. Якщо на основі цих даних ми зможемо побудувати найточнішу прогнозну класифікаційну модель, тоді зможемо й оптимізувати такі показники надійності банківських рейтингів: коефіцієнт прогнозної здатності (КПЗ, формула (2.1)); рівень точності (РТ, формула (2.9)); площа під кривою ROC (AUC, формула (2.12)); індекс Піетра (PI, формула (2.15)); Баєсівський рівень помилки (BER, формула (2.18)); ентропійні показники (формули (2.19-2.23)); показник Бріера (BS, формула (2.24)).
Проблемним моментом у застосуванні класичних інструментів класифікації є відносно мала кількість спостережень у дефолтному класі (DF-1 = 1) – лише 79 дефолтних точок, тоді як факторних ознак – 132. Відповідно ми повинні попередньо відібрати близько 20 найбільш дискримінантних ознак. Тільки після цього можна будувати класифікаційні моделі і перевіряти їх точність, вторинно добираючи класифікаційні ознаки. Всі розрахунки проведені нами у прикладному пакеті програмного забезпечення для статистичних розрахунків «Scilab», який є безкоштовним програмним забезпеченням з відкритим кодом і призначений для наукових досліджень.
Для швидкої фільтрації факторних ознак [189] розглядається класифікаційна здатність кожної ознаки окремо із застосуванням t-статистики. Відповідно для кожної ознаки можна встановити р-значення (p-value), яке показує ймовірність того, що ця факторна ознака є випадковою для розрізнення двох класів. Якщо факторна змінна має p-value 10%, то це означає, що з ймовірністю 10% ця змінна не є пояснювальною, а розрізняє два класи випадково. Тому що менше p-value, то надійнішою є факторна ознака.
Кумулятивна функція розподілу кількості факторних ознак залежно від р-значення для ЗМ-132 при прогнозуванні DF-1 наведена на рис. 4.2.
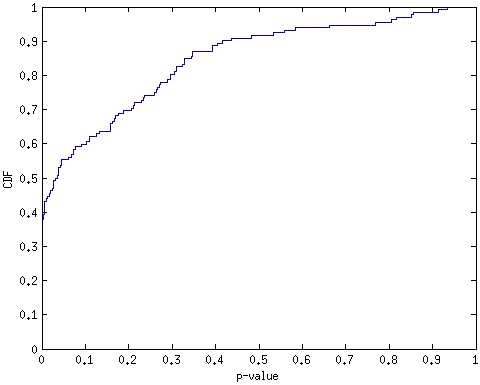
З рис. 4.2 видно, що приблизно 45% факторних ознак мають p-value менше 0,01 (1%), тобто лише стосовно 60 із 132 факторних ознак існує висока ймовірність того, що вони є невипадковими (пояснювальними) змінними для класифікації. Решту факторних ознак можна не розглядати.
Щоб із 60 факторних ознак із прийнятним р-значенням відібрати близько 20 найбільш дискримінантних ознак, ми загальну кількість квартальних спостережень (3934) поділяємо випадковим чином на дві вибірки так, щоб у кожній із них були приблизно однакові частки кожного з класів («0» та «1»). Перша вибірка називається тренувальною, і до неї входить 3134 точок. Друга вибірка є тестовою, і до неї входить 800 точок. Частка дефолтних банків у тренувальній вибірці становить (79–16)/3134 = 2% і в тестовій – 16/800 = 2%. Тренувальну вибірку ми використовуємо для побудови квадратичної дискримінантної функції (КДФ), а тестову – для перевірки класифікаційної точності побудованої функції.
Проведений аналіз показав, що вибір КДФ є оптимальним із точки зору мінімізації помилки класифікації (MCE – misclassification error). MCE розраховується як відношення кількості точок, які були класифіковані неправильно, до їх загальної кількості. При цьому, як уже зазначалося, помилки можуть бути двох типів:
- помилка першого типу – якщо банк, що не банкрутує, класифікується як банкрут;
- помилка другого типу – якщо банк, що банкрутує, класифікується як фінансово стійкий.
Для побудови КДФ тренувальна вибірка п’ять разів повторно випадковим чином поділяється на субтренувальну і повірочну вибірки. До субтренувальної входить 2508 точок, а до повірочної – 626 точок. Повірочна вибірка використовується у процесі «навчання» КДФ для розрахунку тренувальних значень <i>MCE</i>. Алгоритм навчання полягає в послідовному перебиранні всіх 60 факторних ознак із крос-валідацією на повірочних вибірках. Та сукупність ознак, яка мінімізує <i>МСЕ</i> на повірочних вибірках, вважається оптимальною для даної кількості ознак. Таким чином ми можемо на осі Х відкласти кількість оптимальних відібраних ознак, а на осі <i>Y</i> – тренувальні <i>MCE</i>. На цей же графік доцільно вивести тестові <i>MCE</i>, тобто помилки класифікації КДФ, яка навчена на тренувальній вибірці із застосуванням алгоритму крос-валідації [170], на тестовій вибірці у 800 точок. Відповідні графіки наведені на рис. 4.3.
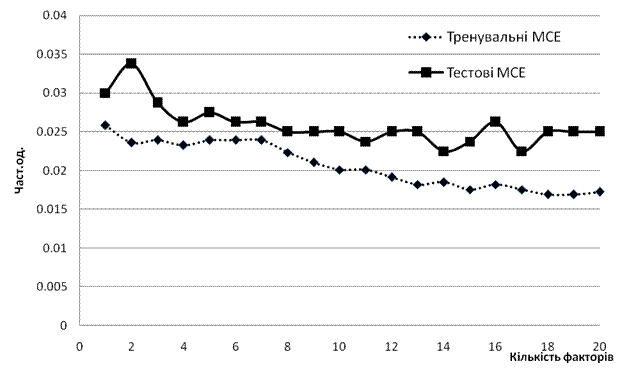
З рис. 4.3 видно, що оптимальними є 17 факторів, які мінімізують тестову MCE. До відібраних факторів належать TA, K47, H6, MR23, H31, TСВД, K38, K48, TR, K7m, K2m, K17, TВВП, LR, K1, K1m, K29. КДФ, яка враховує ці 17 факторів (позначимо її КДФ(17)), на тестовій вибірці у 800 точок припускається 18 помилок. Матрицю збігів для КДФ(17) наведено в табл. 4.2.
Таблиця 4.2. Матриця збігів КДФ(17) на тестовій вибірці у 800 точок для DF-1
| Фактичне значення класів | Спрогнозовані КДФ(17) класи | |
| «0» | «1» | |
| «0» | 776 | 8 |
| «1» | 10 | 6 |
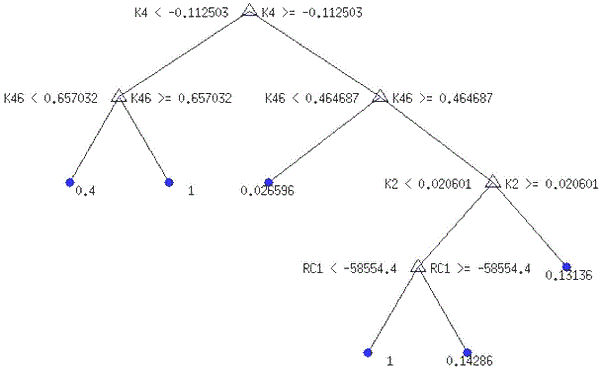
З табл. 4.2 видно, що КДФ(17) на тестовій вибірці у 800 точок припускається 8 помилок першого типу і 10 помилок другого типу. Помилка класифікації у цьому випадку становитиме: MCE = (10+8)/800 = 2,25%. Оскільки отримане значення помилки класифікації для КДФ(17) може залежати від методу випадкового поділу генеральної сукупності на тренувальну і тестову вибірки, ми випадковим чином формуємо 5 примірників тренувальної (3148 точок) і тестової (786 точок) вибірок і ще раз проводимо крос-валідацію КДФ(17). У підсумку ми отримали п’ять значень кількостей помилкових прогнозів: 18, 35, 16, 11, 20. Середнє значення становить 20 помилок, тому реальне середнє значення помилки класифікації для КДФ(17) становить MCE = 20/786 = 2,54%. Відносно малі значення MCE не повинні вводити в оману, оскільки з матриці збігів (табл. 4.2) чітко видно, що більше половини дефолтів спрогнозувати неможливо. За формулою (2.1) і даними матриці збігів можна розрахувати КПЗ для КДФ(17): КПЗ = (776·6+0,5·6·8+0,5·10·776)/(784·16) = 0,6824. Значення КПЗ більше за 0,5 вважається прийнятним для рейтингової моделі, проте в нас є лише два рейтингові класи («дефолтний» і «недефолтний»), тому ми повинні дещо модифікувати розрахунок КПЗ, щоб збільшити ціну помилки. КПЗ з більшою ціною за похибки (КПЗ-с) будемо розраховувати за формулою (2.1), тільки R(ij) дорівнюватиме 0, а не 0,5, якщо рейтингові класи двох порівнюваних банків збігатимуться. Таким чином, ми розраховуємо КПЗ-с для КДФ(17): КПЗ-с = (776·6)/(784·16) = 0,3712. Отже, для КДФ(17) КПЗ-с чітко показує, що спрогнозувати дефолт банку у наступному кварталі з прийнятною точністю неможливо (КПЗ-с>0,5).
Наступні інструменти інтелектуального аналізу даних, які ми повинні перевірити на відібраних 17 факторних ознаках, називаються «деревами рішень». Повне дерево рішень, яке навчене на тренувальній вибірці (3134 точок) на основі відібраних вище 17 факторних ознак, ми позначаємо ДР(17, 3134). Матриця збігів ДР(17, 3134) на тестовій вибірці у 800 точок наведена в табл. 4.3.
Таблиця 4.3. Матриця збігів ДР(17, 3134) на тестовій вибірці у 800 точок для DF-1
| Фактичне значення класів | Спрогнозовані ДР(17, 3134) класи | |
| «0» | «1» | |
| «0» | 780 | 4 |
| «1» | 9 | 7 |
З табл. 4.3 видно, що ДР(17, 3134) на тестовій вибірці у 800 точок припускається 4 помилки першого типу і 9 помилок другого типу. Помилка класифікації у цьому випадку становитиме MCE = (9+4)/800 = 1,63%. При крос-валідації ДР(17, 3134) середнє значення MCE становить 2,31%, що вказує на те, що у процесі навчання сформоване дерево рішень занадто сильно підлаштувалося під випадкову навчальну вибірку і частково втратило здатність узагальнювати інформацію. КПЗ для ДР(17, 3134) на тестовій вибірці становить 0,7162 і КПЗ-с – 0,4353. Отже, для ДР(17, 3134) КПЗ-с показує, що спрогнозувати дефолт банку у наступному кварталі з прийнятною точністю (КПЗ-с>0,5) неможливо.
Щоб дерево рішень не запам’ятовувало дані, а виявляло корисну узагальнену інформацію в даних, його «підрізають» [174], тобто зменшують кількість «термінальних вузлів». Оптимальну кількість термінальних вузлів обирають шляхом поступового їх зменшення і розрахунку відповідних крос-валідаційних MCE (рис. 4.4).
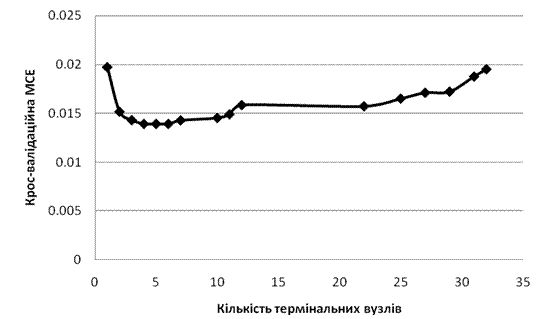
З рис. 4.4 видно, що оптимальне дерево рішень повинно мати чотири термінальні вузли. Таке дерево рішень наведене на рис. 4.5, умовно ми його позначаємо ДР-4тв (DF-1).
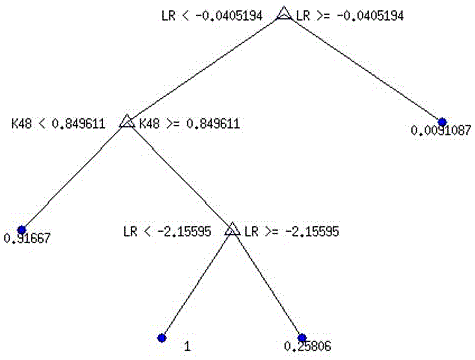
З рис. 4.5 видно, що оптимальне дерево рішень враховує лише дві факторні ознаки: коефіцієнт левериджу (LR) і відношення дохідних активів до зобов’язань (К48). Матриця збігів ДР-4тв на тестовій вибірці у 800 точок наведена в табл. 4.4.
Таблиця 4.4. Матриця збігів ДР-4тв на тестовій вибірці 800 точок для DF-1
| Фактичне значення класів | Спрогнозовані ДР-4тв класи | |
| «0» | «1» | |
| «0» | 784 | 0 |
| «1» | 10 | 6 |
З табл. 4.4 видно, що ДР-4тв на тестовій вибірці у 800 точок припускається 0 помилок першого типу і 10 помилок другого типу. Помилка класифікації у цьому випадку становитиме MCE = (10+0)/800 = 1,25%. При крос-валідації ДР-4тв середнє значення MCE становить 2,31%, що вказує на те, що в процесі навчання сформоване дерево рішень занадто сильно підлаштувалося під випадкову навчальну вибірку і частково втратило здатність узагальнювати. КПЗ для ДР-4тв на тестовій вибірці становить 0,6875 і КПЗ-с – 0,3750. Отже, для ДР-4тв КПЗ-с показує, що спрогнозувати дефолт банку в наступному кварталі з прийнятною точністю неможливо.
Тепер ми повинні перевірити, чи при зменшенні кількості факторних ознак з 17 до 2 для побудови ДР-4тв не були втрачені важливі фактори, які могли б поліпшити якість прогнозу DF-1. Для цього ми використовуємо алгоритм побудови «лісу дерев» [148], який дає змогу виявити важливість кожного із 17 факторів при визначенні рейтингових класів банків у тестових крос-валідаційних випадкових вибірках (рис. 4.6).
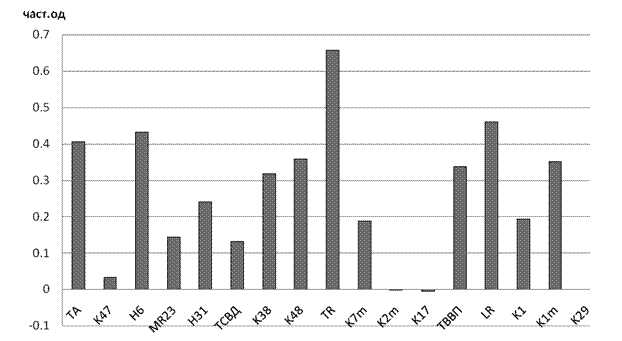
З рис. 4.6 видно, що частину факторів можна відкинути, тому ми залишаємо лише факторні ознаки, рівень важливості яких більший за 0,2. На основі відібраних 9 факторних ознак будуємо і тестуємо нове дерево рішень ДР(9) і нову КДФ(9). До факторів, які враховують ДР(9) і КДФ(9), належать TA, H6, H31, K38, K48, TR, TВВП, LR, K1m.
Матриця збігів для КДФ(9) наведена в табл. 4.5.
Таблиця 4.5. Матриця збігів КДФ(9) на тестовій вибірці 800 точок для DF-1
| Фактичне значення класів | Спрогнозовані КДФ(9) класи | |
| «0» | «1» | |
| «0» | 776 | 8 |
| «1» | 10 | 6 |
З табл. 4.5 видно, що КДФ(9) на тестовій вибірці у 800 точок припускається 8 помилок першого типу і 10 помилок другого типу. Помилка класифікації у цьому випадку становитиме MCE = (10+8)/800 = 2,25%. КПЗ для КДФ(9, 3134) на тестовій вибірці становить 0,6824 і КПЗ-с – 0,3712. Оскільки отримане значення помилки класифікації для КДФ(9) може залежати від методу випадкового поділу генеральної сукупності на тренувальну і тестову вибірки, ми випадковим чином формуємо п’ять примірників тренувальної (3148 точок) і тестової (786 точок) вибірок і ще раз проводимо крос-валідацію КДФ(9). Таким чином ми отримали п’ять значень кількостей помилкових прогнозів: 32, 320, 27, 19, 19. Середнє значення становить 83,4 помилок, тому реальне середнє значення помилки класифікації для КДФ(9) становить MCE = 83,4/786 = 10,61%. Отже, для КДФ(9) КПЗ-с і середнє значення MCE чітко показують, що спрогнозувати дефолт банку у наступному кварталі з прийнятною точністю неможливо. Крім того, середнє значення MCE для КДФ(9) значно більше за середнє значення MCE для КДФ(17).
Матриця збігів ДР(9, 3134) на тестовій вибірці у 800 точок наведена в табл. 4.6.
Таблиця 4.6. Матриця збігів ДР(9, 3134) на тестовій вибірці у 800 точок для DF-1
| Фактичне значення класів | Спрогнозовані ДР(9, 3134) класи | |
| «0» | «1» | |
| «0» | 781 | 3 |
| «1» | 10 | 6 |
З табл. 4.6 видно, що ДР(9, 3134) на тестовій вибірці у 800 точок припускається 3 помилки першого типу і 10 помилок другого типу. Помилка класифікації у цьому випадку становитиме MCE = (10+3)/800 = 1,63%. При кросвалідації ДР(9, 3134) середнє значення MCE становить 2,29%, що вказує на те, що в процесі навчання сформоване дерево рішень занадто сильно підлаштувалося під випадкову навчальну вибірку і частково втратило здатність узагальнювати. КПЗ для ДР(9, 3134) на тестовій вибірці становить 0,6856 і КПЗ-с – 0,3736. Отже, для ДР(9, 3134) КПЗ-с чітко показує, що спрогнозувати дефолт банку у наступному кварталі з прийнятною точністю неможливо.
Розрахунки показали, що ДР(9) і КДФ(9) не є кращими за ДР-4тв. Відповідно, ми повинні встановити, наскільки точність ДР-4тв залежить від випадковості поділу загальної сукупності квартальних точок (3934) на тренувальну (3134 точок) і тестову (800 точок) вибірки. Тому ми формуємо випадковим чином 20 сукупностей тренувальних і тестових вибірок. Тренувальні вибірки відкидаємо і не використовуємо їх для навчання дерев рішень, а тестові використовуємо для валідації вже побудованого ДР-4тв, яке наведене на рис. 4.5. Отримані результати наведено в табл. 4.7.
Таблиця 4.7. Валідація ДР-4тв для прогнозування DF-1 на 20 випадкових тестових вибірках
| Номер випадкової тестової вибірки | Кількість правильно спрогнозованих «недефолтних» банків | Кількість помилок першого типу | Кількість помилок другого типу | Кількість правильно спрогнозованих «дефолтних» банків |
| 1 | 783 | 0 | 13 | 4 |
| 2 | 783 | 1 | 9 | 7 |
| 3 | 783 | 0 | 11 | 6 |
| 4 | 783 | 0 | 9 | 8 |
| 5 | 784 | 0 | 9 | 7 |
| 6 | 783 | 1 | 10 | 6 |
| 7 | 783 | 0 | 12 | 5 |
| 8 | 784 | 0 | 10 | 6 |
| 9 | 783 | 0 | 7 | 10 |
| 10 | 784 | 0 | 10 | 6 |
| 11 | 783 | 0 | 10 | 7 |
| 12 | 783 | 0 | 11 | 6 |
| 13 | 781 | 2 | 11 | 6 |
| 14 | 782 | 1 | 8 | 9 |
| 15 | 783 | 0 | 9 | 8 |
| 16 | 783 | 0 | 8 | 9 |
| 17 | 783 | 1 | 10 | 6 |
| 18 | 783 | 1 | 12 | 4 |
| 19 | 782 | 1 | 10 | 7 |
| 20 | 782 | 1 | 10 | 7 |
| Середнє значення | 782,9 | 0,45 | 9,95 | 6,7 |
| Стандартне відхилення | 0,71818485 | 0,60480532 | 1,46808145 | 1,55935209 |
З табл. 4.7 видно, що недефолтні у наступному кварталі банки визначаються доволі точно. В середньому 10 банків із 17 збанкрутілих помилково класифікуються як недефолтні, і тільки 7 із 17 (або 41%) збанкрутілих банків класифікуються правильно. Середнє значення КПЗ-с для ДР-4тв становить 0,4016, при цьому мінімальне значення – 0,2353 і максимальне – 0,5882. Значний діапазон КПЗ-с для ДР-4тв та стандартне відхилення у 22% від середнього значення вказують на значну залежність КПЗ-с від способу формування тестової вибірки. Загалом за показником КПЗ-с ДР-4тв не можна вважати надійною моделлю для прогнозування банкрутств банків у наступному кварталі.
Перевагою ДР-4тв над іншими моделями є те, що якщо банку присвоєно дефолтний клас, то він із ймовірністю приблизно у 88% збанкрутує у наступному кварталі. ДР-4тв є обережною моделлю в плані мінімізації помилок першого типу, тобто дефолтні категорії надійним банкам фактично не присвоюються. Проте ДР-4тв часто присвоює недефолтну категорію банкам, які банкрутують, у середньому 10 із 17 збанкрутілих банків отримують недефолтну категорію. При цьому, середня ймовірність того, що в недефолтній категорії виявиться збанкрутілий банк становить 9,95/(9,95+782,9) = 1,25%. Загалом, виходячи з принципу обережності, недефолтні оцінки ДР-4тв не варто сприймати як надійні. А до дефолтних рейтингових категорій, які присвоєні ДР-4тв, треба ставитися як до фактичної констатації банкрутства банків у наступному кварталі.
Отже, ДР-4тв здатне виявити приблизно лише 40% дефолтних банків у наступному кварталі, проте ті банки, які виявлені майже з 90% ймовірністю банкрутують у наступному кварталі. Таким чином ДР-4тв може бути сильним сигналізатором переддефолтного стану банку.
Вище ми детально описали спосіб пошуку оптимальних моделей присвоєння банківських рейтингів із застосуванням сучасних інструментів інтелектуального аналізу. Деталі реалізації описаних алгоритмів можна знайти в посиланнях. Надалі ми не наводимо всі проміжні розрахунки, а лише представляємо вже відібрані оптимальні моделі присвоєння рейтингових категорій банкам та їх характеристики надійності.
Аналогічно до DF-1 перевіряємо, чи можна спрогнозувати банкрутство банку протягом наступних двох кварталів за його фінансовими показниками в поточному кварталі. Таким чином, ми розглядаємо підсумкову змінну DF-2, яка набуває значення «0», якщо банк не банкрутує протягом наступних двох кварталів, і значення – «1», якщо банк банкрутує протягом наступних двох кварталів. Проведені нами розрахунки показали, що оптимальним методом для прогнозування DF-2 є дерево рішень з 15 термінальними вузлами ДР-15тв (DF-2), побудоване шляхом «підрізання» дерева рішень ДР(27), яке враховувало 27 попередньо відібраних факторів за допомогою квадратичного дискримінантного аналізу. Оскільки подати ДР-15тв у графічній формі складно через велику кількість термінальних вузлів, описуємо його у текстовій формі:
- якщо K19<6,30918, то вузол 2, інакше якщо K19≥6,30918, то вузол 3;
- якщо K53<0,661223, то вузол 4, інакше якщо K53≥0,661223, то вузол 5;
- якщо K68<0,259515, то вузол 6, інакше якщо K68≥0,259515, то вузол 7;
- якщо K1m<0,330208, то вузол 8, інакше якщо K1m≥0,330208, то вузол 9;
- DF-2 = 0,333333;
- якщо TСЦ<1,16233, то вузол 10, інакше якщо TСЦ≥1,16233, то вузол 11;
- DF-2 = 1;
- DF-2 = 0,25;
- DF-2 = 0,971429;
- якщо K27<0,738007, то вузол 12, інакше якщо K27≥0,738007, то вузол 13;
- якщо K68<-1,42981, то вузол 14, інакше якщо K68≥-1,42981, то вузол 15;
- якщо K7m<-0,0850029, то вузол 16, інакше якщо K7m≥-0,0850029, то вузол 17;
- DF-2 = 1;
- DF-2 = 1;
- якщо TA<0,753597 то вузол 18, інакше якщо TA≥0,753597, то вузол 19;
- якщо K1m<0,208473, то вузол 20, інакше якщо K1m≥0,208473, то вузол 21;
- якщо TСВД<1,08486, то вузол 22, інакше якщо TСВД≥1,08486, то вузол 23;
- DF-2 = 0,555556;
- DF-2 = 0,0694444;
- DF-2 = 0;
- DF-2 = 0,555556;
- якщо КК<0,0678431, то вузол 24, інакше якщо КК≥0,0678431, то вузол 25;
- DF-2 = 0,00395844;
- якщо K17<0,0440968, то вузол 26, інакше якщо K17≥0,0440968, то вузол 27;
- DF-2 = 0,0199147;
- якщо K67<0,00220528, то вузол 28, інакше якщо K67≥0,00220528, то вузол 29;
- DF-2 = 0,0769231;
- DF-2 = 1;
- DF-2 = 0,25.
Валідаційні тести ДР-15тв наведені в табл. 4.8.
Таблиця 4.8. Валідація ДР-15тв для прогнозування DF-2 на 20 випадкових тестових вибірках
| Номер випадкової тестової вибірки | Кількість правильно спрогнозованих «недефолтних» банків | Кількість помилок першого типу | Кількість помилок другого типу | Кількість правильно спрогнозованих «дефолтних» банків |
| 1 | 765 | 6 | 16 | 13 |
| 2 | 770 | 2 | 17 | 11 |
| 3 | 767 | 4 | 13 | 16 |
| 4 | 768 | 3 | 17 | 12 |
| 5 | 769 | 3 | 15 | 13 |
| 6 | 770 | 2 | 9 | 19 |
| 7 | 769 | 2 | 15 | 14 |
| 8 | 770 | 2 | 9 | 19 |
| 9 | 769 | 2 | 17 | 12 |
| 10 | 770 | 2 | 15 | 13 |
| 11 | 766 | 5 | 14 | 15 |
| 12 | 770 | 1 | 14 | 15 |
| 13 | 768 | 3 | 15 | 14 |
| 14 | 764 | 7 | 13 | 16 |
| 15 | 769 | 2 | 14 | 15 |
| 16 | 768 | 3 | 15 | 14 |
| 17 | 771 | 1 | 13 | 15 |
| 18 | 770 | 2 | 12 | 16 |
| 19 | 766 | 5 | 15 | 14 |
| 20 | 768 | 3 | 16 | 13 |
| Середнє значення | 768,35 | 3 | 14,2 | 14,45 |
| Стандартне відхилення | 1,899445903 | 1,622214211 | 2,261811105 | 2,089447169 |
З табл. 4.8 видно, що недефолтні уподовж наступних двох кварталів банки визначаються доволі точно. В середньому 14 банків із 29 збанкрутілих помилково класифікуються як недефолтні і приблизно 15 із 29 (або 50%) збанкрутілих банків класифікуються правильно. Середнє значення КПЗ-с для ДР-15тв становить 0,5029, при цьому мінімальне значення – 0,3918 і максимальне – 0,6768. Значний діапазон КПЗ-с для ДР-15тв та стандартне відхилення у 15,2% від середнього значення вказують на значну залежність КПЗ-с від способу формування тестової вибірки. Загалом за показником КПЗ-с ДР-15тв не можна вважати надійною моделлю для прогнозування банкрутств банків упродовж наступних двох кварталів. Хоч ДР-15тв і не виявляє половини збанкрутілих банків протягом наступних двох кварталів, ця модель має вищі показники надійності за ДР-4тв для DF-1.
Середня ймовірність того, що банк, якому ДР-15тв присвоїло дефолтний клас, не збанкрутує протягом наступних двох кварталів, становить приблизно 3/18 = 0,1667 ≈ 16,7%. Тобто, якщо ДР-15тв присвоює банку дефолтний клас, то він з понад 80% ймовірністю банкрутує протягом наступних двох кварталів. Отже, недефолтні оцінки ДР-15тв не повинні сприйматися як надійні. А до дефолтних рейтингових категорій, які присвоєні ДР-15тв, треба ставитися як до сильного про високу ймовірність банкрутства банків протягом наступних двох кварталів.
За допомогою описаного методу з’ясовано, що оптимальною моделлю для прогнозування дефолту банку у наступні три квартали є ДР-6тв (DF-3) (рис. 4.7).
Оптимальною моделлю для прогнозування дефолту банку у наступні чотири квартали є ДР-10тв (DF-4), яке описується у текстовій формі так:
- якщо LR<-0,0405194, то вузол 2, інакше якщо LR≥-0,0405194, то вузол 3;
- якщо H3-1<-0,181084, то вузол 4, інакше якщо H3-1≥-0,181084, то вузол 5;
- якщо K68<-1,5717, то вузол 6, інакше якщо K68≥-1,5717, то вузол 7;
- DF-4 = 0,972973;
- якщо TR<-0,059867, то вузол 8, інакше якщо TR≥-0,059867, то вузол 9;
- якщо TСЦ<1,01961, то вузол 10, інакше якщо TСЦ≥1,01961, то вузол 11;
- якщо TСВД<1,10828, то вузол 12, інакше якщо TСВД≥1,10828, то вузол 13;
- DF-4 = 0,153846;
- DF-4 = 1;
- DF-4 = 0;
- DF-4 = 1;
- якщо K46<0,464355, то вузол 14, інакше якщо K46≥0,464355, то вузол 15;
- DF-4 = 0,0124378;
- якщо РК1<-4,69515, то вузол 16, інакше якщо РК1≥-4,69515, то вузол 17;
- якщо MR23<98, то вузол 18, інакше якщо MR23≥98, то вузол 19;
- DF-4 = 1;
- DF-4 = 0,0659091;
- DF-4 = 0,112676;
- DF-4 = 0,435484.
Підсумкові характеристики надійності оптимальних моделей прогнозування банкрутства українських банків у наступні періоди за умов макроекономічної нестабільності наведено в табл. 4.9.
Таблиця 4.9. Надійнісні характеристики моделей прогнозування банкрутства банків
| Цільовий показник | DF-1 | DF-2 | DF-3 | DF-4 |
| Оптимальна модель | ДР-4тв | ДР-15тв | ДР-6тв | ДР-10тв |
| Характеристики моделі | ||||
| КПЗ-с середній | 0,4016 | 0,5029 | 0,2025 | 0,2877 |
| КПЗ-с максимальний | 0,5882 | 0,6768 | 0,3333 | 0,4107 |
| КПЗ-с мінімальний | 0,2353 | 0,3918 | 0,125 | 0,1997 |
| Стандартне відхилення (Ст. в.) КПЗ-с | 0,0895 | 0,0764 | 0,0526 | 0,0565 |
| Ст. в. КПЗ-с / КПЗ-с середній, % | 22,27 | 15,2 | 25,97 | 19,64 |
| Середня кількість правильно спрогнозованих «неде-фолтних» банків | 782,9 | 768,35 | 760,5 | 747,7 |
| Ст. в. кількості правильно спрогнозованих «неде-фолтних» банків / Середня кількість правильно спрогнозованих «недефолтних» банків, % | 0,0917 | 0,2472 | 0,0674 | 0,1794 |
| Середня кількість помилок 1-го типу | 0,45 | 3 | 0 | 1,7 |
| Ст. в. кількості помилок 1-го типу / Середня кіль-кість помилок 1-го типу, % | 134,4 | 54,07 | 0 | 85,56 |
| Середня кількість помилок 2-го типу | 9,95 | 14,2 | 31,5 | 36 |
| Ст. в. кількості помилок 2-го типу / Середня кіль-кість помилок 2-го типу, % | 14,75 | 15,93 | 6,71 | 7,65 |
| Середня кількість правильно спрогнозованих «де-фолтних» банків | 6,7 | 14,45 | 8 | 14,6 |
| Ст. в. кількості правильно спрогнозованих «дефолт-них» банків / Середня кількість правильно спрогно-зованих «дефолтних» банків, % | 23,27 | 14,46 | 25,97 | 20,05 |
| Середнє значення КПЗ | 0,7006 | 0,7505 | 0,6013 | 0,6430 |
| Середня частка помилкових прогнозів (MCE), % | 1,3 | 2,15 | 3,94 | 4,71 |
З табл. 4.9 видно, що всі моделі прогнозування банкрутства банків у майбутніх періодах мають високі середні значення КПЗ, що підтверджує їх хорошу дискримінантну спроможність за КПЗ. Середні частки помилкових прогнозів мають низькі значення тільки через відносно незначну кількість дефолтів. За середнім значенням КПЗ-с найкращою є модель ДР-15тв (DF-2), проте за кількістю термінальних вузлів перевага може надаватися ДР-4тв (DF-1), зокрема у випадках, коли дерево рішень використовується в управлінні банком. Меншу кількість вузлів людина сприймає легше, тому управлінцям банків, які аналізують дерева рішень, легше визначити цільові показники діяльності банку. Інформація, яка міститься в дереві рішень, дає змогу менеджерам також встановити, в яких межах повинні перебувати цільові фінансові показники банку, щоб мінімізувати ймовірність банкрутства.
Щоб перевірити, чи можливо максимізувати надійність банківських рейтингів за показником КПЗ-м, перевіряємо, чи можна спрогнозувати рівень рентабельності активів банку за нерозподіленим прибутком у наступному кварталі на підставі його фінансових показників поточного кварталу. Отже, розглядаємо підсумкову змінну RA-1, яка набуває значення «0», якщо банк у наступному кварталі має рентабельність активів за нерозподіленим прибутком більшу за середню для банківської системи, і значення «1», якщо банк у наступному кварталі має рентабельність активів за нерозподіленим прибутком меншу за середню для банківської системи. Нагадаємо, що для розрахунку КПЗ-м банки поділено на дві групи:
- ті, у яких через відповідну кількість кварталів після укладання рейтингів рентабельність активів за нерозподіленим прибутком більша за середню для банківської системи;
- ті, у яких через відповідну кількість кварталів після укладання рейтингів рентабельність активів за нерозподіленим прибутком менша за середню для банківської системи, або банки, що збанкрутували упродовж охопленого показником часового горизонту.
Потім показник КПЗ-м розраховується за формулою (2.1).
За допомогою рекомендованого нами методу з’ясовано, що оптимальною моделлю для прогнозування рівня рентабельності банку в наступному кварталі є ДР-4тв (RA-1) (рис. 4.8).
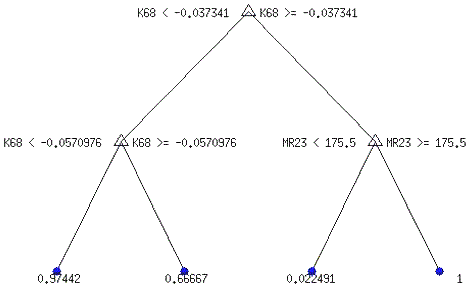
З рис. 4.8 видно, що для прогнозування рівня рентабельності банку у наступному кварталі значення мають діапазони поточної рентабельності за нерозподіленим прибутком (К68) і поточне місце банку в банківській системі за чистим прибутком, що є цілком очікуваним із точки зору формальної логіки.
Нецілі значення термінальних вузлів необхідно сприймати як оцінку ймовірності того, що у наступному кварталі рентабельність активів банку за нерозподіленим прибутком буде меншою за середню для банківської системи.
Аналогічно до RA-1 перевіряємо, чи можна спрогнозувати рентабельність активів банку за нерозподіленим прибутком через два квартали на підставі його фінансових показників поточного кварталу. Отже, розглядаємо підсумкову змінну RA-2, яка набуває значення «0», якщо банк через два квартали має рентабельність активів за нерозподіленим прибутком більшу за середню для банківської системи, і значення «1», якщо банк через два квартали має рентабельність активів за нерозподіленим прибутком меншу за середню для банківської системи. Розрахунки показали, що оптимальною моделлю для прогнозування рентабельності банку через два квартали є ДР-5тв (RA-2) (рис. 4.9).
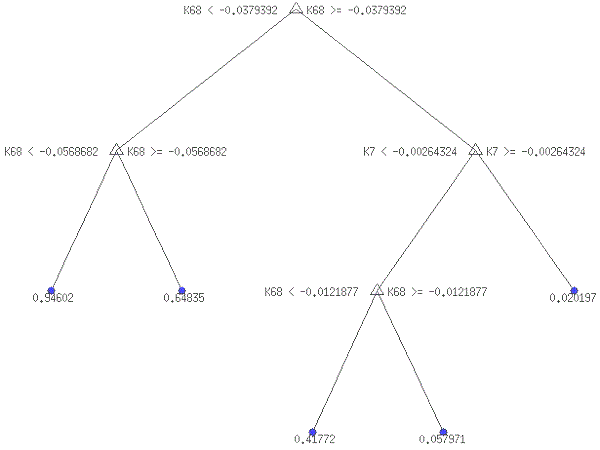
З рис. 4.9 видно, що для прогнозування рентабельності банку через два квартали значення мають діапазони поточної рентабельності за нерозподіленим прибутком (К68) і поточні діапазони відношення чистого прибутку до середнього значення зважених за ризиком активів, згідно з підходами НБУ (К7).
Для змінної RA-3, яка набуває значення «0», якщо банк через три квартали має рентабельність активів за нерозподіленим прибутком більшу за середню для банківської системи, і значення «1», якщо банк через три квартали має рентабельність активів за нерозподіленим прибутком меншу за середню для банківської системи, оптимальною моделлю є наведено на рис. 4.10 ДР-5тв (RA-3).
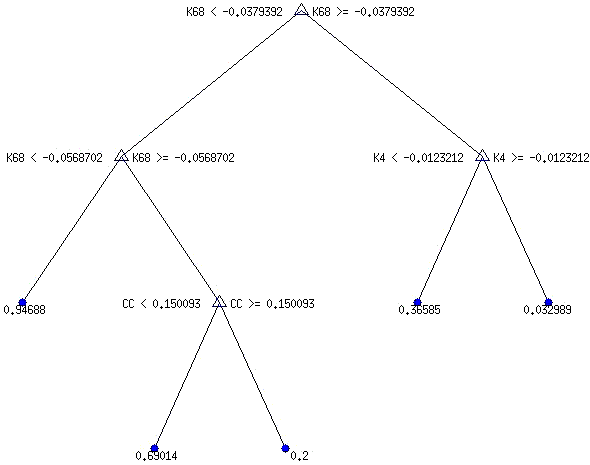
З рис. 4.10 видно, що для прогнозування рентабельності банку через три квартали значення мають діапазони поточної рентабельності за нерозподіленим прибутком (К68), поточні діапазони коефіцієнта Кука (СС) і діапазони поточної рентабельності активів (К4).
Для змінної RA-4, яка набуває значення «0», якщо банк через чотири квартали має рентабельність активів за нерозподіленим прибутком більшу за середню для банківської системи, і значення «1», якщо банк через чотири квартали має рентабельність активів за нерозподіленим прибутком меншу за середню для банківської системи, оптимальною моделлю є наведена на рис. 4.11 ДР-7тв (RA-4).
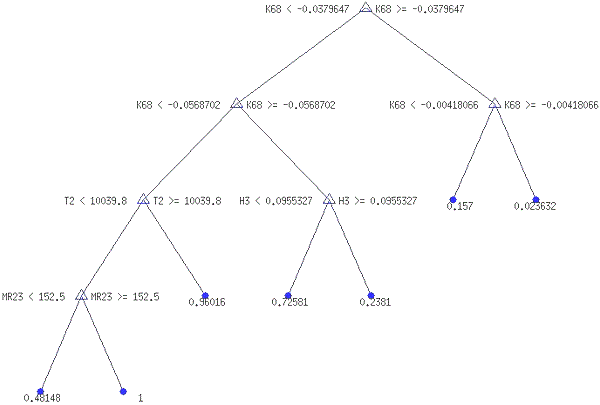
З рис. 4.11 видно, що для прогнозування рентабельності банку через чотири квартали значення мають діапазони поточної рентабельності за нерозподіленим прибутком (К68), поточні діапазони Н3, діапазони капіталу другого рівня (Т2) і місце банку в банківській системі за чистим прибутком (MR23).
Підсумкові характеристики надійності оптимальних моделей прогнозування рентабельності активів за нерозподіленим прибутком українських банків у наступні періоди за умов макроекономічної нестабільності наведені в табл. 4.10.
Таблиця 4.10. Надійнісні характеристики моделей прогнозування класів рентабельності банків
| Цільовий показник | RA-1 | RA-2 | RA-3 | RA-4 |
| Оптимальна модель | ДР-4тв | ДР-5тв | ДР-5тв | ДР-7тв |
| Характеристики моделі | ||||
| КПЗ-с середній | 0,8770 | 0,8008 | 0,7889 | 0,7324 |
| КПЗ-с максимальний | 0,9084 | 0,8455 | 0,8573 | 0,8032 |
| КПЗ-с мінімальний | 0,8451 | 0,7408 | 0,7260 | 0,6966 |
| Стандартне відхилення (Ст.в.) КПЗ-с | 0,019 | 0,029 | 0,035 | 0,03 |
| Ст. в. КПЗ-с / КПЗ-с середній, % | 2,17 | 3,59 | 4,46 | 4,1 |
| Середня кількість правильно спрогнозованих банків, рентабельність активів за нерозподіленим прибутком яких більша за середню для банківської системи | 645,7 | 643,4 | 643,3 | 648,15 |
| Ст. в. кількості правильно спрогнозованих «рентабель-них»* банків / Середня кількість правильно спрогнозо-ваних «рентабельних» банків, % | 0,52 | 0,55 | 0,43 | 0,44 |
| Середня кількість помилок 1-го типу | 12,6 | 14,9 | 14,9 | 9,05 |
| Ст. в. кількості помилок 1-го типу / Середня кількість помилок 1-го типу, % | 25,67 | 23,94 | 17,81 | 31,56 |
| Середня кількість помилок 2-го типу | 15 | 25,6 | 27,35 | 36,75 |
| Ст. в. кількості помилок 2-го типу / Середня кількість помилок 2-го типу, % | 18,1 | 15,49 | 18,39 | 12,07 |
| Середня кількість правильно спрогнозованих банків, рентабельність активів за нерозподіленим прибутком яких менша за середню для банківської системи | 126,7 | 116,1 | 114,45 | 106,05 |
| Ст. в. кількості правильно спрогнозованих «нерента-бельних»* банків / Середня кількість правильно спрог-нозованих «рентабельних» банків, % | 2,08 | 3,41 | 4,4 | 4,1 |
| Середнє значення КПЗ-м (для порівняння див. табл. 2.7) | 0,9375 | 0,8984 | 0,8922 | 0,8645 |
| Середня частка помилкових прогнозів (MCE), % | 3,45 | 5,06 | 5,28 | 5,73 |
* під «рентабельними» маються на увазі банки, рентабельність активів за нерозпо-діленим прибутком яких у прогнозному періоді вища за середню для банківської системи; під «нерентабельними» маються на увазі банки, рентабельність активів за нерозподіленим прибутком яких у прогнозному періоді нижча за середню для банківської системи.
З табл. 4.10 видно, що отримані за допомогою моделі за КПЗ-с прогнози рівнів рентабельностей банків є надійними. Це означає, що можна з високою точність спрогнозувати, чи буде рентабельність активів банку за нерозподіленим прибутком вищою або нижчою за середню для банківської системи. Своєючергого, це означає, що можна створити модель присвоєння банківських рейтингів, яка буде надійною за КПЗ-м.
У підрозділі 3.1 було показано, що надійність банківських рейтингів вітчизняних рейтингових агентств за показником КПЗ-м є низькою (табл. 3.4, 3.5). Зрозуміло, що найважче передбачити рівень рентабельності активів банку через рік (RA-4), проте навіть ДР-7тв (RA-4) показує доволі точні результати. Наприклад, ймовірність того, що серед банків, яким ДР-7тв (RA-4) присвоїло «нульовий» клас, будуть банки, рентабельність активів яких за нерозподіленим прибутком через рік менша за середню для банківської системи, становить 36,75/(36,75+648,15) = 5,37%. Ймовірність того, що серед банків, яким ДР-7тв (RA-4) присвоїло «перший» клас, будуть банки, рентабельність активів яких за нерозподіленим прибутком через рік більша за середню для банківської системи, становить 9,05/(106,05+9,05) = 7,86%. Отже, рівень помилок є прийнятним.
Щоб перевірити, чи можливо максимізувати надійність банківських рейтингів за показником ARP (рівень точності за чистим прибутком (формула (2.33))), перевіряємо, чи можна спрогнозувати знак чистого прибутку банку у наступному кварталі за його фінансовими показниками в поточному кварталі. Для цього розглядаємо підсумкову змінну NP-1, яка набуває значення «0», якщо банк за наступний квартал має чистий прибуток, і значення «1», якщо банк за наступний квартал має чистий збиток (від’ємний чистий прибуток).
За допомогою нашого методу з’ясовано, що оптимальною для прогнозування прибутковості банку в наступному кварталі є модель ДР-9тв (NP-1), у текстовій формі описана так:
- якщо K7m<-0,00223513, то вузол 2, інакше якщо K7m≥-0,00223513, то вузол 3;
- якщо MR23<141,5, то вузол 4, інакше якщо MR23≥141,5, то вузол 5;
- якщо TСЦ<1,13653, то вузол 6, інакше якщо TСЦ≥1,13653, то вузол 7;
- якщо TСЦ<1,14998, то вузол 8, інакше якщо TСЦ≥1,14998, то вузол 9;
- якщо MКП<128,5, то вузол 10, інакше якщо MКП≥128,5, то вузол 11;
- якщо K7m<0,00413887, то вузол 12, інакше якщо K7m≥0,00413887, то вузол 13;
- якщо MR23<130,5, то вузол 14, інакше якщо MR23≥130,5, то вузол 15;
- NP-1 = 0,286885;
- NP-1 = 0,78125;
- NP-1 = 0,723549;
- NP-1 = 0,422222;
- якщо K7m<1,36309, то вузол 16, інакше якщо K7m≥1,36309, то вузол 17;
- NP-1 = 0,268908;
- NP-1 = 0,328358;
- NP-1 = 0,866667;
- NP-1 = 0,275281;
- NP-1 = 0,126171.
Оптимальною для прогнозування знака чистого прибутку банку за наступні два квартали є модель ДР-9тв (NP-2), яка у текстовій формі описана так:
- якщо K7<-0,00105064, то вузол 2, інакше якщо K7≥-0,00105064, то вузол 3;
- якщо MR23<139,5, то вузол 4, інакше якщо MR23≥139,5, то вузол 5;
- якщо K7m<0,00413887, то вузол 6, інакше якщо K7m≥0,00413887, то вузол 7;
- якщо K57<0,157843, то вузол 8, інакше якщо K57≥0,157843, то вузол 9;
- якщо K42<0,20009, то вузол 10, інакше якщо K42≥0,20009, то вузол 11;
- якщо TСЦ<1,11883, то вузол 12, інакше якщо TСЦ≥1,11883, то вузол 13;
- NP-2 = 0,312997;
- NP-2 = 0,247788;
- NP-2 = 0,553846;
- NP-2 = 0,767442;
- NP-2 = 0,482353;
- NP-2 = 0,13929;
- якщо MR23<139,5, то вузол 14, інакше якщо MR23≥139,5, то вузол 15;
- якщо MД<90,5, то вузол 16, інакше якщо MД≥90,5, то вузол 17;
- NP-2 = 1;
- NP-2 = 0,368;
- NP-2 = 0,140741.
Для змінної NP-3, яка набуває значення «0», якщо банк за наступні три квартали має додатний чистий прибуток, і значення «1», якщо банк за наступні три квартали має від’ємний чистий прибуток, оптимальною є наведена на рис. 4.12 модель ДР-8тв (NP-3).
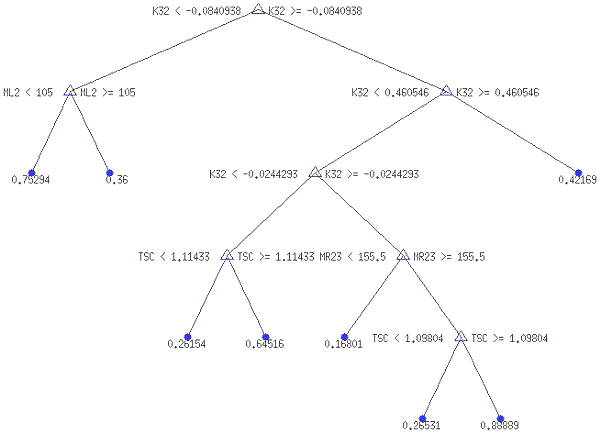
На рис. 4.12 ML2 – це місце банку в банківській системі за розміром термінових депозитів і TSC – річний темп зростання споживчих цін. Із рис. 3.12 видно, що знак чистого прибутку за наступні три квартали залежить від поточних діапазонів загальної рентабельності (К32), місця банку в банківські системі за терміновими депозитами (ML2), темпу споживчих цін (TSC) і місця банку в банківській системі за чистим прибутком (MR23). При цьому немає жодного термінального вузла з чистою рейтинговою категорією (0 або 1). Це означає, що ДР-8тв (NP-3) підтверджує ймовірність того, що за наступні три квартали банк отримає збитки.
Для змінної NP-4, яка набуває значення «0», якщо банк за наступні чотири квартали має додатній чистий прибуток, і значення «1», якщо банк за наступні чотири квартали має від’ємний чистий прибуток, оптимальною є наведена на рис. 4.13 модель ДР-6тв (NP-4).
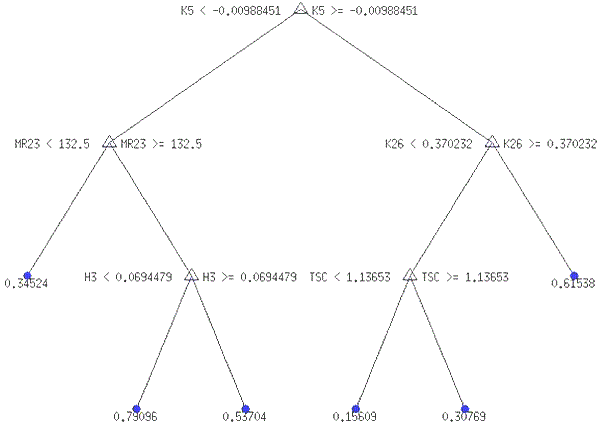
З рис. 4.13 видно, що знак чистого прибутку за наступні чотири квартали залежить від поточних діапазонів відношення чистого прибутку до середнього значення власного капіталу (К5), темпу споживчих цін (TSC), місця банку в банківській системі за чистим прибутком (MR23), відношення сформованих резервів до активів (К26) і співвідношення регулятивного капіталу до сукупних активів (Н3).
Підсумкові характеристики надійності оптимальних моделей прогнозування знака чистого прибутку українських банків у наступні періоди за умов макроекономічної нестабільності наведені в табл. 4.11.
Таблиця 4.11. Надійнісні характеристики моделей прогнозування прибутковості банків
| Цільовий показник | NP-1 | NP-2 | NP-3 | NP-4 |
| Оптимальна модель | ДР-9тв | ДР-9тв | ДР-8тв | ДР-6тв |
| Характеристики моделі | ||||
| КПЗ-с середній | 0,3273 | 0,3160 | 0,2939 | 0,3510 |
| КПЗ-с максимальний | 0,3662 | 0,3641 | 0,3372 | 0,4476 |
| КПЗ-с мінімальний | 0,2652 | 0,2731 | 0,2526 | 0,3001 |
| Стандартне відхилення (Ст. в.) КПЗ-с | 0,0277 | 0,0260 | 0,0207 | 0,0325 |
| Ст. в. КПЗ-с / КПЗ-с середній, % | 8,46 | 8,24 | 7,05 | 9,27 |
| Середня кількість правильно спрогнозованих банків, чистий прибуток яких є додатним | 571 | 559,7 | 564,85 | 565,15 |
| Ст. в. кількості правильно спрогнозованих прибутко-вих банків / Середня кількість правильно спрогнозова-них прибуткових банків, % | 0,94 | 0,70 | 0,88 | 0,95 |
| Середня кількість помилок 1-го типу | 26,55 | 29,85 | 27,55 | 36,85 |
| Ст. в. кількості помилок 1-го типу / Середня кількість помилок 1-го типу, % | 20,47 | 13,24 | 17,76 | 14,53 |
| Середня кількість помилок 2-го типу | 133,1 | 140,4 | 143,6 | 123,35 |
| Ст. в. кількості помилок 2-го типу / Середня кількість помилок 2-го типу, % | 4,4 | 4,07 | 3,23 | 5,31 |
| Середня кількість правильно спрогнозованих банків, чистий прибуток яких є від’ємним | 69,35 | 70,05 | 64 | 73,65 |
| Ст. в. кількості правильно спрогнозованих збиткових банків / Середня кількість правильно спрогнозованих збиткових банків, % | 8,4 | 8,28 | 7,24 | 8,89 |
| Середнє значення КПЗ за чистим прибутком | 0,6491 | 0,6411 | 0,6309 | 0,6563 |
| Середня частка помилкових прогнозів (MCE), % | 19,96 | 21,28 | 21,39 | 20,05 |
З табл. 4.11 видно, що помилка класифікації при прогнозуванні знаків чистого прибутку банків у майбутніх періодах становить приблизно 20%, тобто спрогнозувати прибутковість чи збитковість банку із прийнятною точністю найважче порівняно з іншими прогнозними показниками. При прогнозуванні знака чистого прибутку в наступному кварталі ймовірність того, що серед банків, яким ДР-9тв (NP-1) прогнозує додатний чистий прибуток, виявляться збиткові банки, становить 133,1/(571+133,1) = 18,9%. При цьому ймовірність того, що серед банків, яким ДР-9тв (NP-1) прогнозує у наступному кварталі чистий збиток, виявляться прибуткові банки, становить 26,55/(26,55+69,35) = 27,69%. Отже, якщо ДР-9тв (NP-1) прогнозує у наступному кварталі додатний чистий прибуток, то ймовірність правильного прогнозу становитиме приблизно 80%, але якщо ДР-9тв (NP-1) прогнозує у наступному кварталі чистий збиток, то ймовірність правильного прогнозу становитиме приблизно 70%. Тому при прогнозуванні знака чистого прибутку слід більше довіряти позитивним прогнозам. Середнє значення КПЗ-с приблизно становить 0,31, що вказує на те, що за цим показником моделі прогнозування знака чистого прибутку не є надійним, проте за показником КПЗ за чистим прибутком, який у середньому становить приблизно 0,64, точність зазначених моделей є прийнятною. Зі зростанням часового горизонту прогнозування зростає кількість помилок 1-го типу, що зменшує точність збиткових прогнозів до 67%. Зі зростанням часового горизонту точність прибуткових прогнозів зростає до 82%. Отже, прибуткові прогнози є більш надійними за збиткові. Це означає, що завдання виявити банк, який зазнає збитків у майбутніх періодах, є важким.
Для відкритих методик українських уповноважених рейтингових агентств і РА «Moody’s» побудовані моделі прогнозування DF, RA і NP не показали кращих за ЗМ-132 показників надійності. Це означає, що при застосуванні нашого методу побудови оптимальних моделей укладання банківських рейтингів, який передбачає застосуванням інструментів інтелектуального аналізу, початкова кількість аналізованих фінансових показників банків і макроекономічних показників повинна бути максимальною. При цьому важливе значення є методика розрахунку рекомендованих фінансових показників банків, описана в підрозділі 4.1.
